Эпидемия коронавируса: статистика и математическое моделирование
Дата обновления 17.06.2022 10:00 (Мск)
Данные приведены за период с начала пандемии в России по 16.06.2022
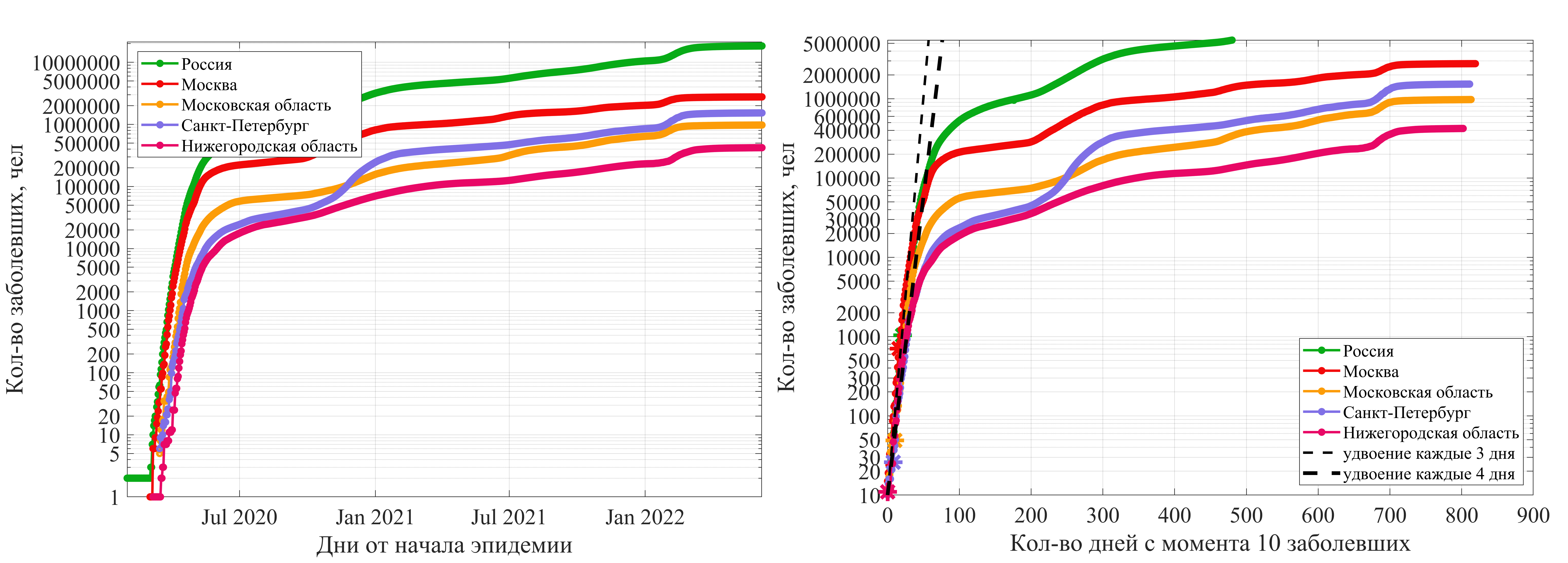
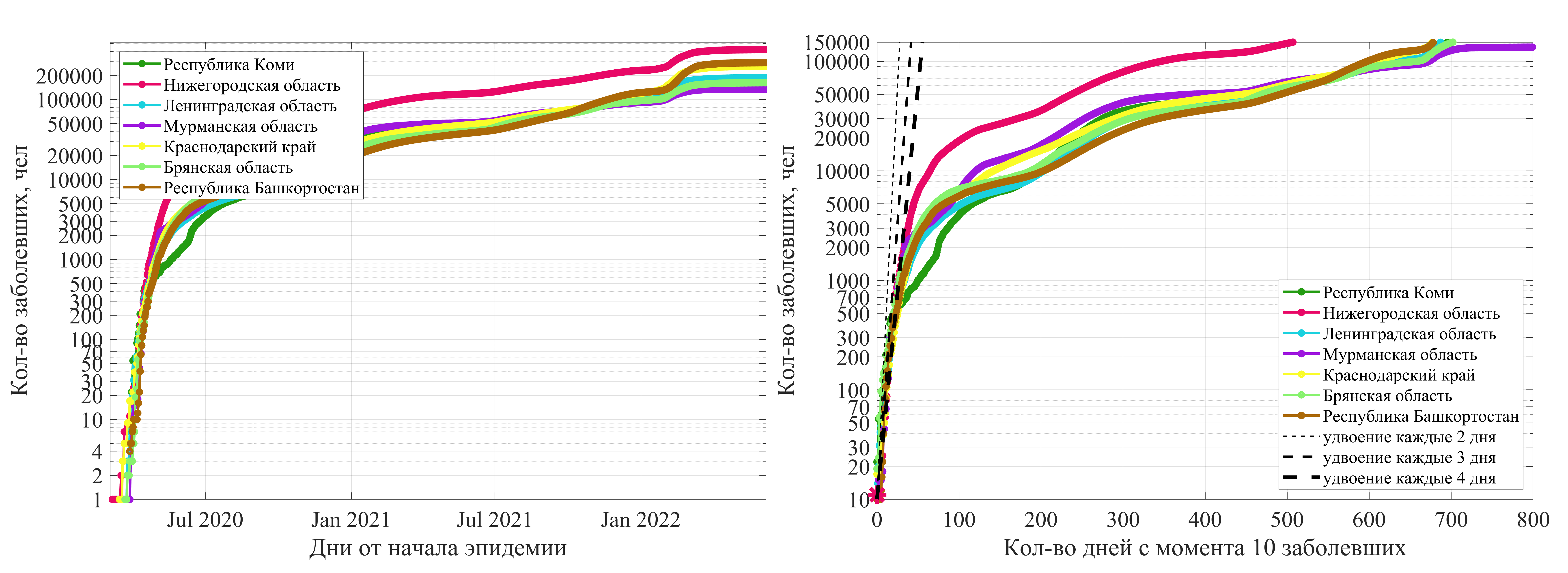
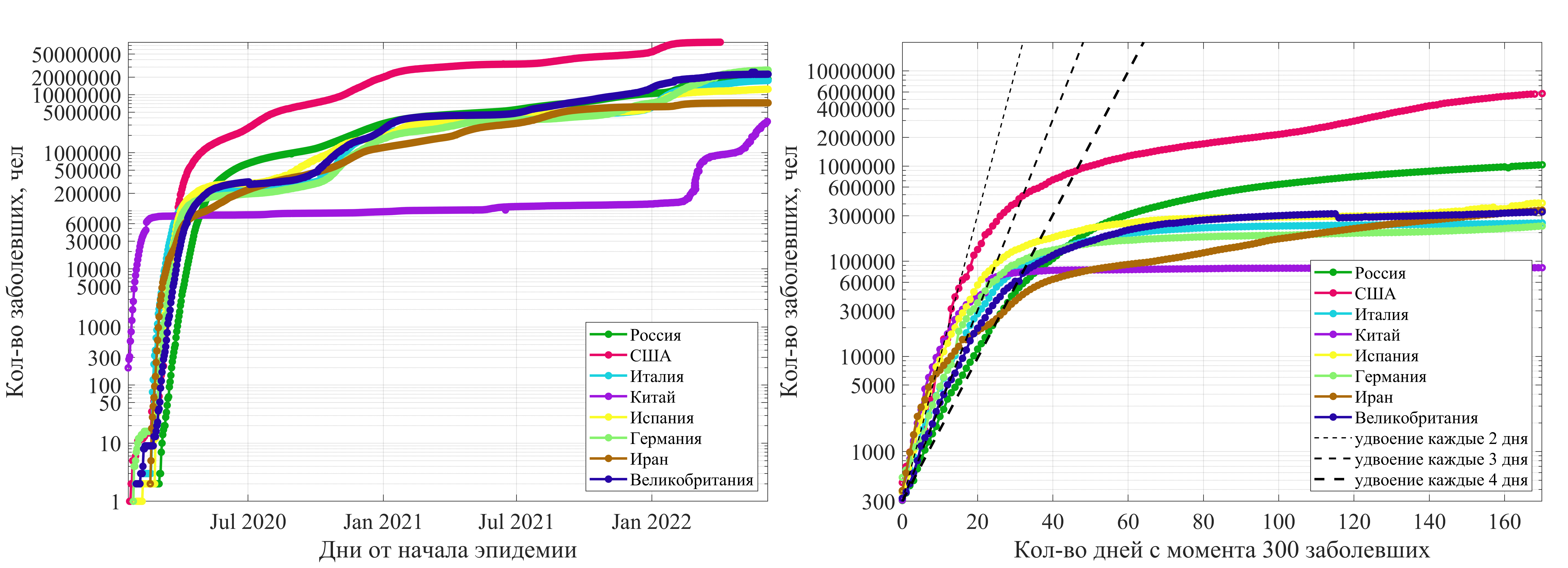
Слева - данные по датам, справа - с момента появления определенного количества заболевших. На всех графиках логарифмический масштаб вертикальной оси. Символом '*' обозначен день начала самоизоляции (28.03.2020). Данные по другим регионам.
Нормированные данные по России и по миру, для стран — число случаев на 1 млн чел, для регионов — число случаев на 1 тыс. чел.
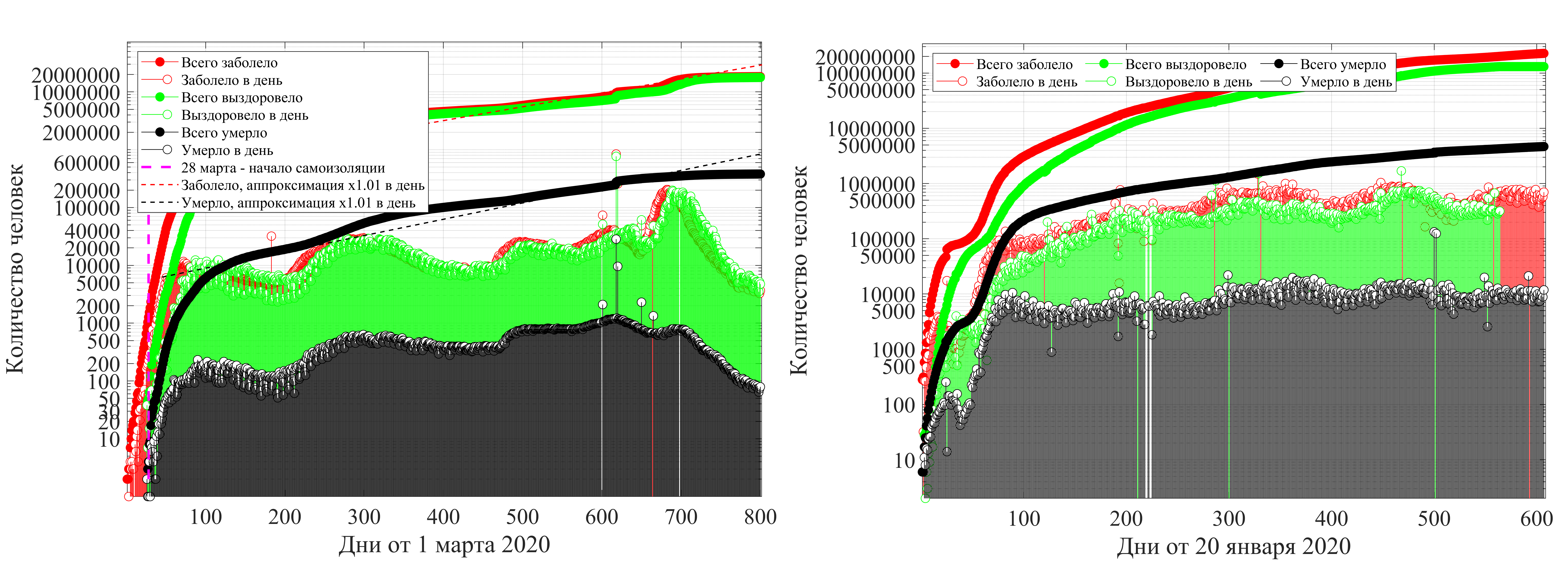
Слева - данные по России, справа - по миру.
Источники данных: стопкоронавирус.рф
Роспотребнадзор
Johns Hopkins Coronavirus Resourse Center
NN.ru
World Health Organisation
ZNAK
Coronavirus-monitor
Worldometr
С простейшими моделями распространения эпидемии можно ознакомиться в работе Куркин А.А., Куркина О.Е., Пелиновский Е.Н. Логистические модели распространения эпидемий // Труды Нижегородского государственного технического университета им. Р.Е. Алексеева. 2020. № 2(129). С. 9-18. https://www.nntu.ru/frontend/web/ngtu/files/nauka/izdaniya/trudy/2020/02/009-018.pdf
Публикации сотрудников в СМИ: Положительный анализ: почему в России растёт заболеваемость COVID-19
Отложенный рост: зараженные попадают в статистику через 20 дней
Вопрос на миллион: удвоится ли число зараженных в России
Первый миллион: о чем говорит цифра зараженных COVID-19 россиян
Весенний отзыв: к началу апреля число больных COVID-19 в Москве упадет вчетверо
Математическое моделирование
Для описания моделей распространения эпидемий используются математические модели разного уровня: от простейших, описывающих только одну характеристику эпидемии (например, число заболевших), до весьма сложных, учитывающих различные характеристики эпидемий, включая возраст и инкубационный период разных групп населения. Основная проблема в применении этих моделей связана с определением коэффициентов (а иногда и функций) в этих моделях на начальном этапе развития эпидемии, когда еще очень мало известно о природе вирусов и как они воздействуют на различные группы населения. Наиболее полные данные (приводимые на официальных сайтах) касаются, числа заболевших, умерших и вылечившихся. Здесь мы применим простейшую модель, основанную на логистической кривой (см., например, статью (Куркин и др., 2020) и литературу в ней), для описания числа заболевших. Это позволит нам определить точность этой модели, оценить заблаговременность определения коэффициентов модели, и выдать прогноз развития эпидемий. Расчетные формулы для нахождения общего числа заболевших (N) и количества заболевших людей в сутки (K) следующие:

где время отсчитывается от начала эпидемии, N0 – начальное число заболевших, N∞– ожидаемое общее число заболевших людей за все время эпидемии, и r – частота распространения эпидемии. Частота распространения эпидемии хорошо определяется на начальном этапе развития эпидемии, а N∞ – уточняется по мере поступления новых данных.
Пример: результаты расчетов для Австрии
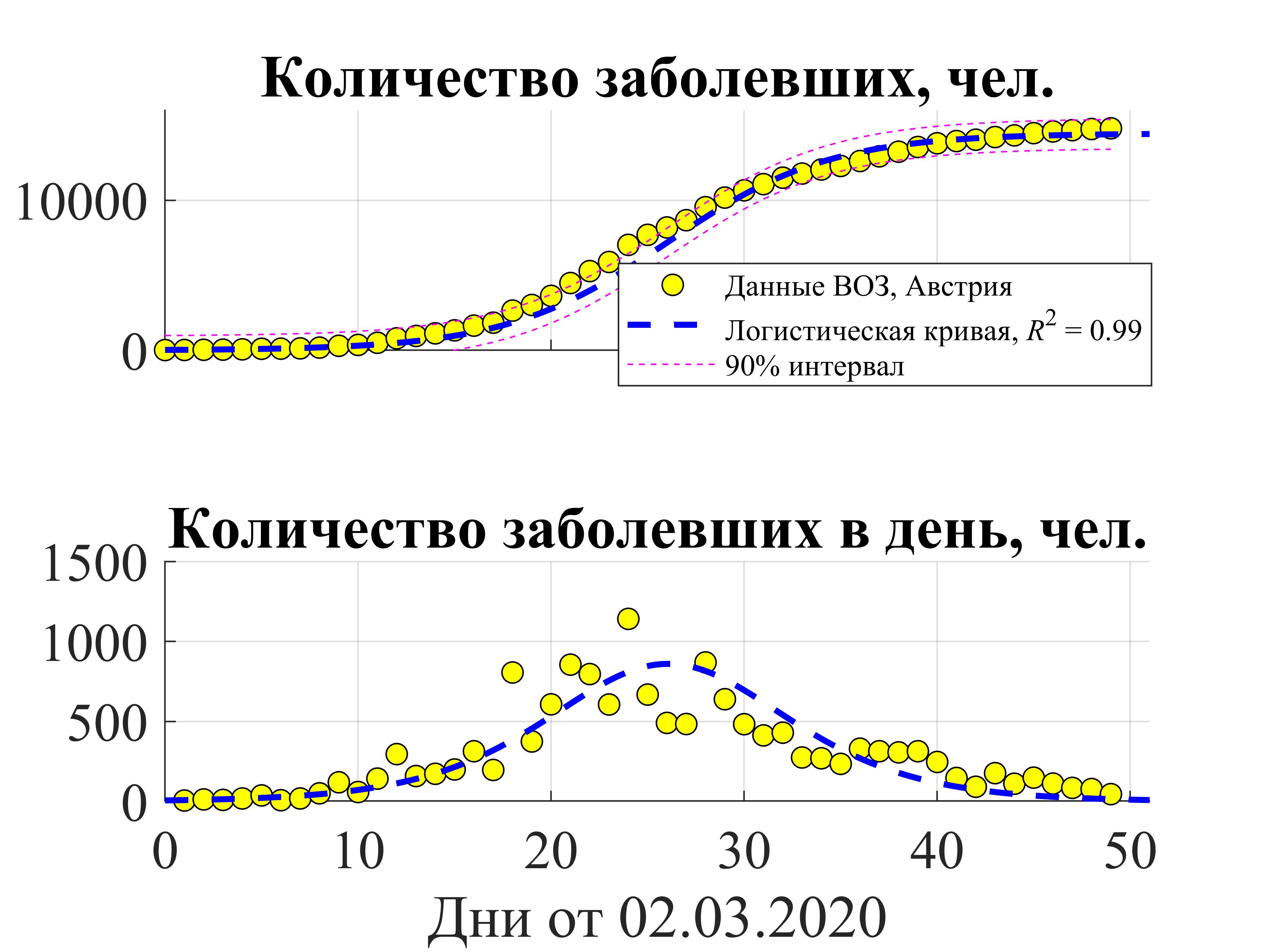
N0 и r определялись по четырем начальным неделям (02.03 – 29.03.2020), а N∞– по оставшимся данным.
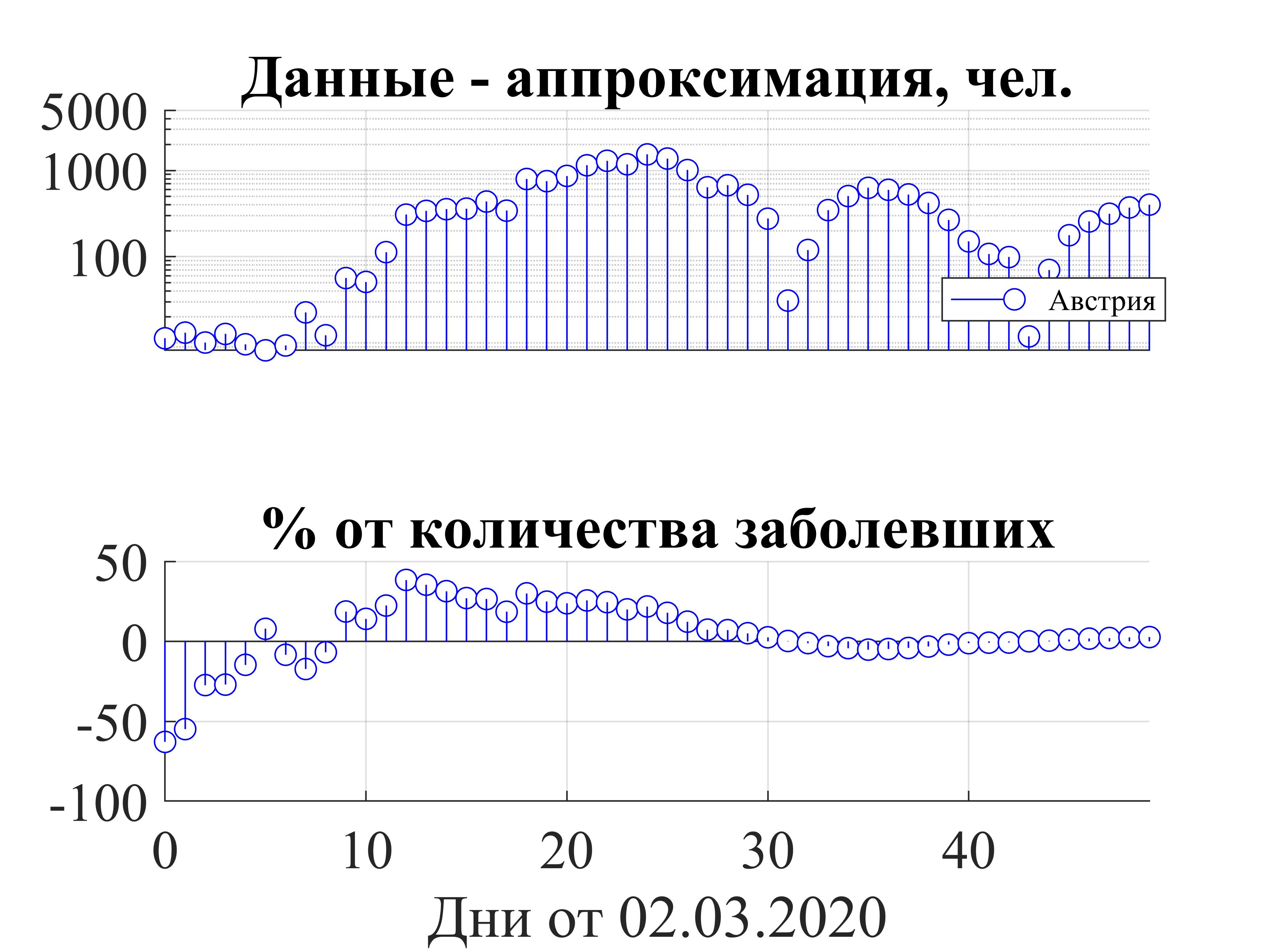
Здесь показана разница между данными и моделью, сверху абсолютное значение, снизу – в %.
Пример: результаты расчетов для Швейцарии: Здесь подбор N0 и r идет по 3 неделям с 6 по 26 марта, а далее подбирается N∞
Пример: результаты расчетов для Китая: Здесь подбор N0 и r идет по 3 неделям с 20 января по 9 февраля, а далее подбирается N∞
Пример: результаты расчетов для Италии: Здесь подбор N0 и r идет по 6 неделям с 23 февраля по 5 апреля, а далее подбирается N∞
Пример: результаты расчетов для Турции: Здесь подбор N0 и r идет по 4 неделям с 17 марта по 13 апреля, а далее подбирается N∞
Пример: результаты расчетов для Голландии: Здесь подбор N0 и r идет по 5 неделям с 2 февраля по 7 марта, а далее подбирается N∞
Участники проекта: Куркин А.А., Пелиновский Е.Н., Епифанова А.С., Кокоулина М.В., Куркина О.Е., Лешехва Е.Н.
Go to project